Quick-Start

This demo is implemented in a single Python file.

This demo illustrates how to:

Create mesh based.
Create functions defined in cells.
Define a list of currents used in the experiment.
Solve Forward Problem.
Solve inverse Problem

Importing

from module1_mesh import*
from module2_forward import*
from module3_inverse import*
from module4_auxiliar import*
import matplotlib.pyplot as plt

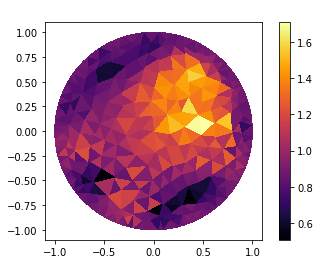
Mesh

mesh_inverse, mesh_direct=MyMesh(r=1, n=8, n_vertex=121) #Genereting mesh
mesh_direct=refine(mesh_direct)                          #Refine again mesh

"Plot"
plt.figure(figsize=(8, 8))
plt.subplot(1,2,1)
plot(mesh_direct);
plt.subplot(1,2,2)
plot(mesh_inverse);

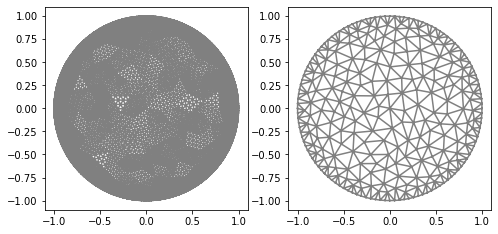
Gamma Function

"Defining gamma"
ValuesCells0=GammaCircle(mesh_direct,3,1,0.35, 0.35, 0.30); #mesh, value_int, value_ex, radius, certerx, certery.

"Plot"
V_DG=FiniteElement('DG',mesh_inverse.ufl_cell(),0) #Descontinous Galerkin degree 0
gamma_direct=plot_figure(mesh_direct, V_DG, gamma0, name="Gamma"); #Just plot my gamma0

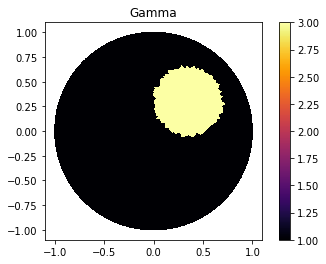
Forward Problem

Eletric Current

"Current"
n_g=6  #Number measurements
I_all=current_method(n_g, value=1, method=1) #Function that returns the current

Solver

"ForwardProblem"
VD=FiniteElement('CG',mesh_direct.ufl_cell(),1)      #Continuos Galerking degree 1
ForwardObject=ForwardProblem(mesh_direct)              #Forward Object
list_u0=ForwardObject.solve_forward(VD, gamma0, I_all) #Solver, Space, gamma and current.

#If you will use it in the inverse problem without noise.
u0_boundary=ForwardObject.boundary_array(mesh_inverse) #Boundary data in the mesh_inverse

plt.figure(figsize=(10, 10))
for i in range(0, n_g):
    plt.subplot(4,4,i+1)
    plot(list_u0[i])

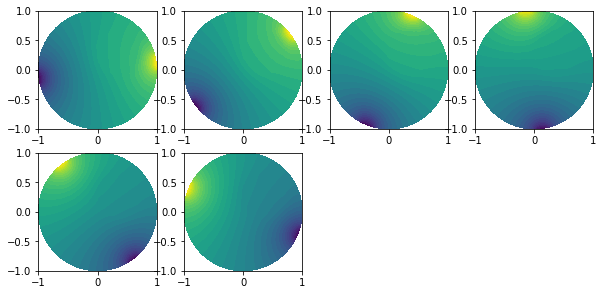
Noise

#Setting noise in the data.
"Noise Parameters"
noise_level=0.005 #0.5%
noise_type='uniform'
seed=1 #Random seed

u0_boundary=ForwardObject.add_noise(noise_level, noise_type, seed, mesh_inverse) #Returns noised data.

Inverse Problem

"Object"
VI=FiniteElement('CG',mesh_inverse.ufl_cell(),1)                   #Creating Object
InverseObject=InverseProblem(mesh_inverse, VI, u0_boundary, I_all) #Add mesh, space, data, current
InverseObject.set_NoiseParameters(tau=2, noise_level=0.005)        #Inform if data is noised
InverseObject.set_solverconfig(step_limit=30)                      #Step Limit

"Solver"
InverseObject.solve_inverse() #Solve

"Getting the result"
gamma_k=InverseObject.gamma_k

"Plot result"
V_DG=FiniteElement('DG',mesh_inverse.ufl_cell(),0)
gamma_k=plot_figure(mesh_inverse, V_DG, gamma_k, name=" ");