Quick-Start
This demo is implemented in a single Python file. Download here: tutorial_quickstart.ipynb
This demo illustrates how to:
Create mesh based in eletrodes
Create functions defined in cells.
Define a list of currents used in the experiment.
Solve Forward Problem.
Solve inverse Problem:
Importing
from EIT_CEM_app import *
%matplotlib inline
Electrodes
O passo inicial para o modelo de eletrodos é definir a região de eletrodos. Para este fim temos a função
electrodes_position() para auxiliar no processo. Espera-se que o dominio seja um círculo, o qual
é necessário saber o raio. Além disso, pergunta-se o número de eletrodos(L) e a área percentual (per_cober) por eles ocupados.
Então os eletrodos serão distribuidos igualmente espaçados na fronteira. Ainda é possível rotacionar a solução
atráves do argumento rotate.:
"Basic Definitions"
r=1 #Circle radius
L=16 #Number of Electrodes
per_cober=0.5 #Percentage of area covered by electrodes
rotate=0 #Rotation
#Return a object with angular position of each electrode
ele_pos=electrodes_position(L, per_cober, rotate)
Mesh
Segundo passo importante é definir a malha a ser trabalhada tanto para o problema direto e inverso. Essa malha é construida em função dos eletrodos. Define-se o refinamento da malha (refine_n), a quantidade de vértices nos eletrodos (n_in) e a quantidade de vértices no gaps (n_out). Através da malha gerada, usa-se a função refine() nativa do FENICS para realizar o refinamento para a malha do problema direto.:
refine_n=8 #Refinement mesh
n_in=8 #Vertex on elec.
n_out=2 #Vertex on gaps (Sometimes it is important.)
mesh_inverse=MyMesh(r, refine_n, n_in, n_out, ele_pos)
mesh_forward=MyMesh(r, refine_n*3, n_in*3, n_out*3, ele_pos)

Gamma Function
Terceiro passo consiste na definição de uma função de condutividade elétrica em função dos elementos da malha.
Para isso usa-se a função GammaCircle() para criar um circulo deslocado da origem de raio 0.5, onde a condutividade
dentro do círculo é 3.0 e fora dele 1.0. A função anteriormente citada apenas cria um vetor onde cada entrada
representA o valor da célula em um elemento, a função CellFunction() é responsável por transformar em uma Expression,
sendo utilizada como uma função no FENICS para resolver o sistema variacional, ou seja transformamos um vetor em uma função.
"Solution Forward problem"
#GammaCircle returns a vector that is a map between elements and their cell values.
ValuesCells0=GammaCircle(mesh_forward,3.0,1.0,0.50, 0.25, 0.25); #mesh, cond_in, cond_out, radius, certerx, cerntery
gamma0=CellFunction(mesh_forward, values=ValuesCells0); #Transform vector to function
A seguir a solução reconstruida no espaço DG.
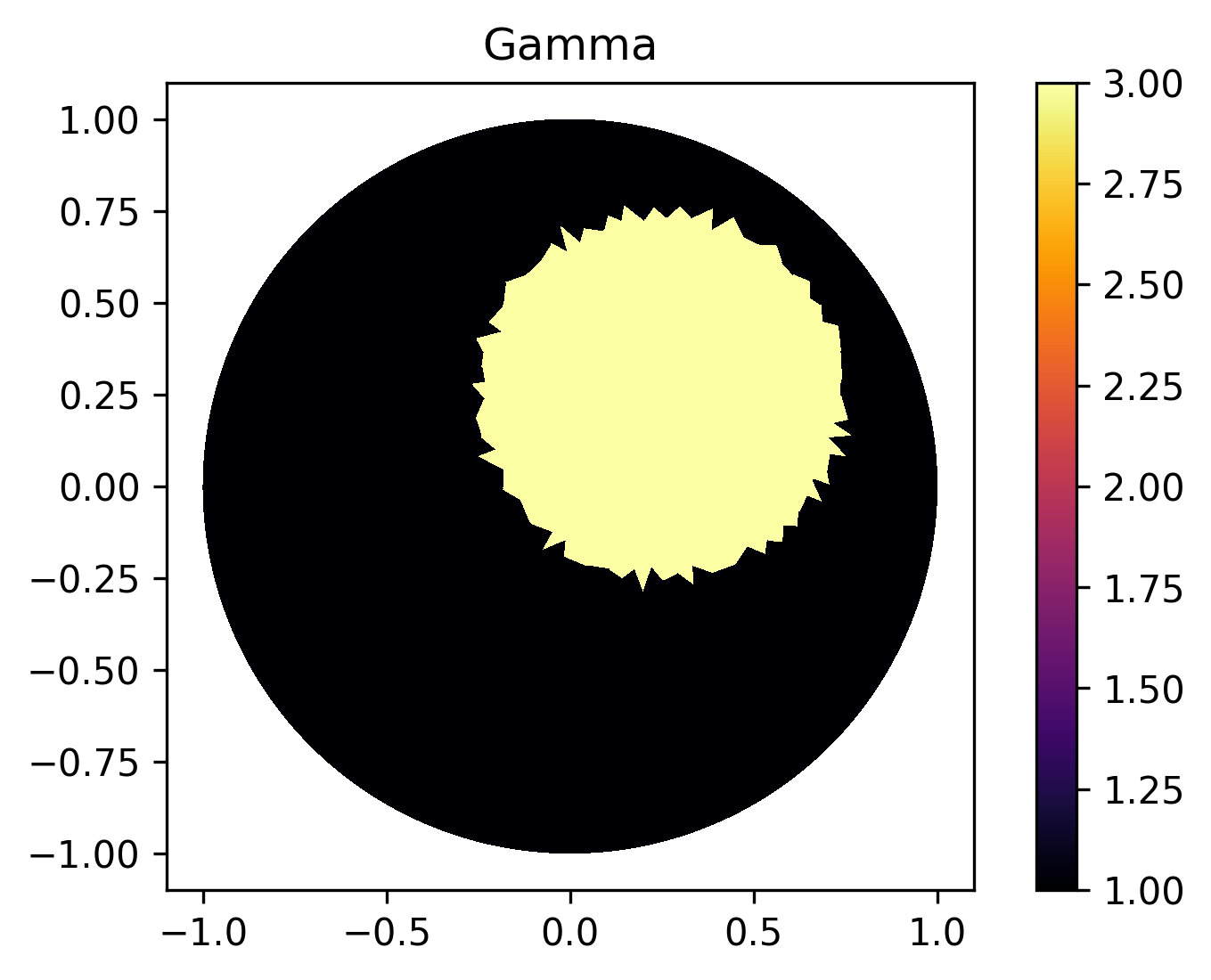
"Plot"
V_DG=FiniteElement('DG',mesh_forward.ufl_cell(),0)
gamma_direct=plot_figure(mesh_forward, V_DG, gamma0, name="Gamma");
Forward Problem
Dado as definições anteriores, já é possível seguir para o problema direto. Basta definir o espaço de funções utilizadas, aqui usamos polinômios de lagrange (CG) de primeira ordem, número de experimentos (l), a impedancia dos eletrodos (z) e as correntes utilizadas (I_all).:
"Forward Problem"
#Definições básicas
z=np.ones(L)*0.025 #Impedance of each electrode
l=L-1 #Numero of experiments
I_all=current_method( L ,l, method=2) #Current
VD=FiniteElement('CG',mesh_forward.ufl_cell(),1) #Solution Space Continous Galerkin
A função current_method() retorna uma array de arrays contendo os valores das correntes nos eletrodos.
Existem outras correntes e elas podem ser verificadas na documentação. Caso queira outro tipo de corrente para o experimento,
basta obedecer o mesmo padrão na hora de fornecer as correntes. Se for só um experimento, só é necessário fornecer uma array simples.:
print(np.array(I_all))
[[ 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. -1.]]
Já com as definições do básicas do problema direto, já é possível resolve-lo. Cria-se o objeto do problema direto
com a classe ForwardProblem fornecendo informações como a malha, posição dos eletrodos e as impedancias.
Após isso usa-se a função .solver_forward() para resolver o problema, usando como argumento o espaço de funções(VD), a função de conduvidade (gamma0),
as correntes elétricas (I_all) e o número de experimentos (l).
#Solver
ForwardObject=ForwardProblem(mesh_forward, ele_pos, z)
list_u0, list_U0 = ForwardObject.solve_forward(VD, gamma0, I_all, l)
list_U0 = DirectProblem.sol_asarray()
As soluções no domínio podem ser plotadas com os comandos a seguir:
plt.figure(figsize=(10, 10))
for i in range(0, l):
plt.subplot(4,4,i+1)
plot(list_u0[i])
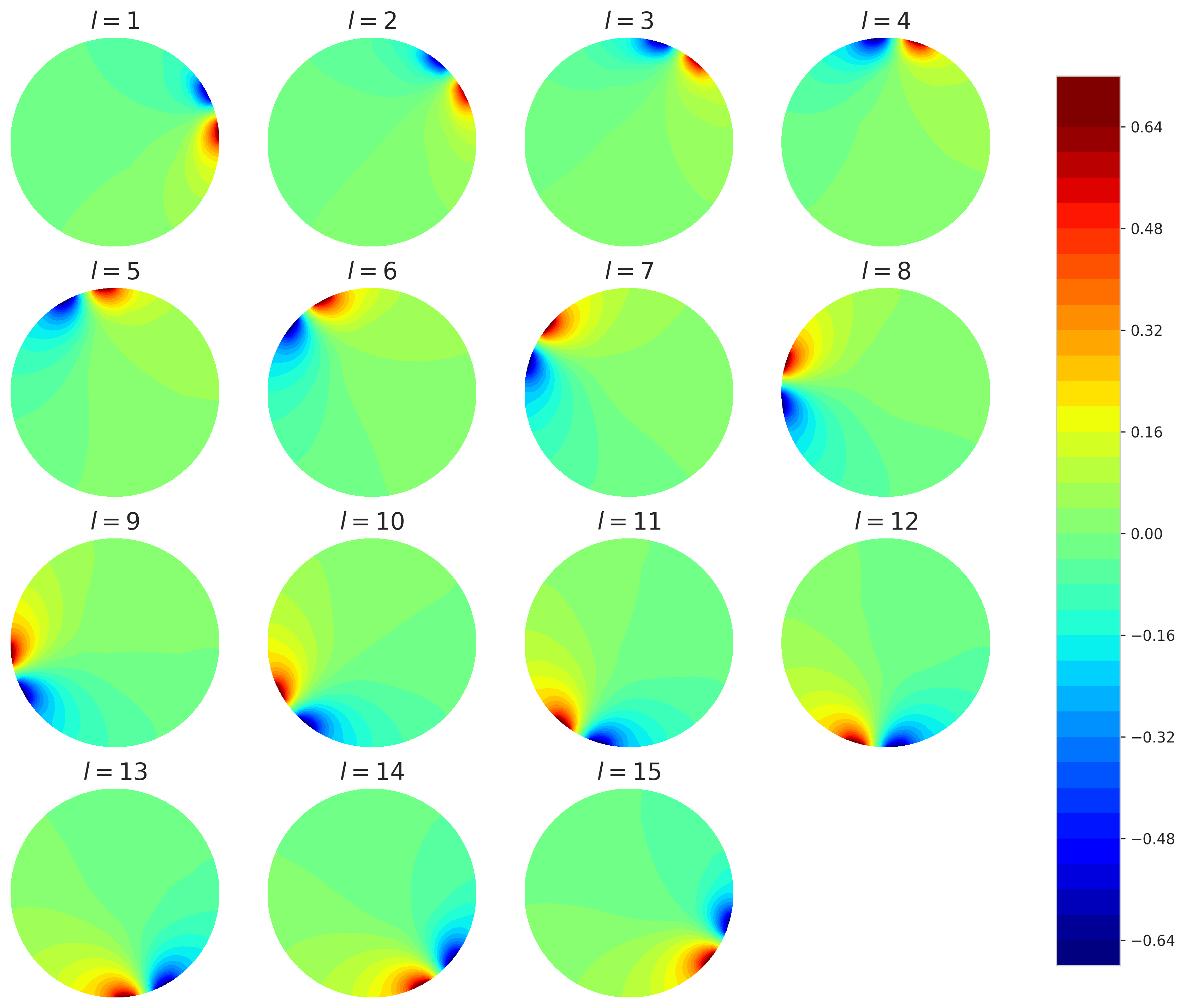
O valor dos potenciais nos eletrodos está contido no vetor list_U0.:
print(list_U0[0:L])
[ 0.74659668 -0.69037383 -0.11527343 -0.06251943 -0.04542257 -0.03537776
-0.02792534 -0.02158871 -0.01562908 -0.00952088 -0.00273239 0.00552806
0.01674227 0.0342237 0.0673924 0.15588032]
Os rúidos nos dados podem ser introduzidos com as seguintes rotinas.:
#Noise add
noise_level=0.01
noise_type='uniform'
if noise_level>1E-10: list_U0_noised = ForwardObject.add_noise(noise_level, noise_type)
list_U0_noised=fn_addnoise(list_U0, noise_level, noise_type, seed=42)
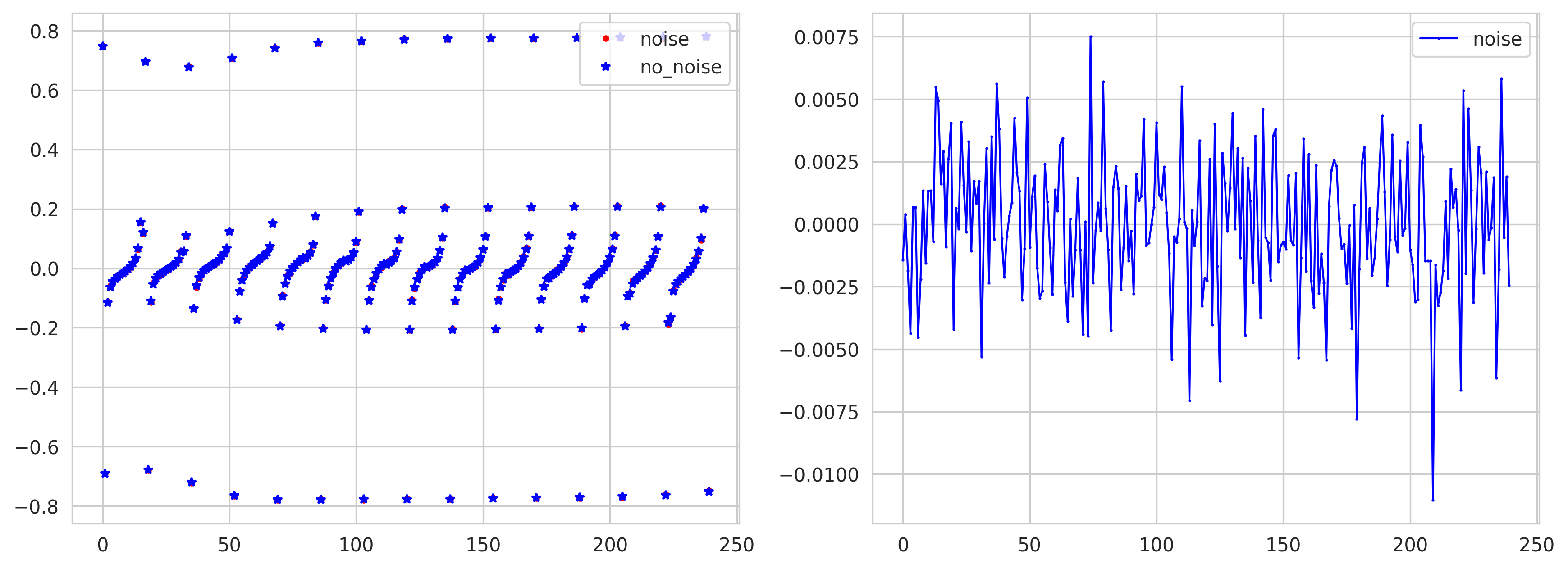
O problema inverso é simples de resolver quando já se possui os eletrodos, a malha, impedâncias e correntes.
Basta fornecer um vetor contendo os valores nos eletrodos (list_U0) ao objeto InverseProblem e chamar a função
solve_inverse().
InverseObject=InverseProblem(mesh_inverse, ele_pos, list_U0_noised, I_all, l, z)
InverseObject.set_solverconfig(step_limit=100)
"Noise Parameters"
tau=1.2
InverseObject.set_NoiseParameters(tau=tau, noise_level=0.01)
InverseObject.solve_inverse()
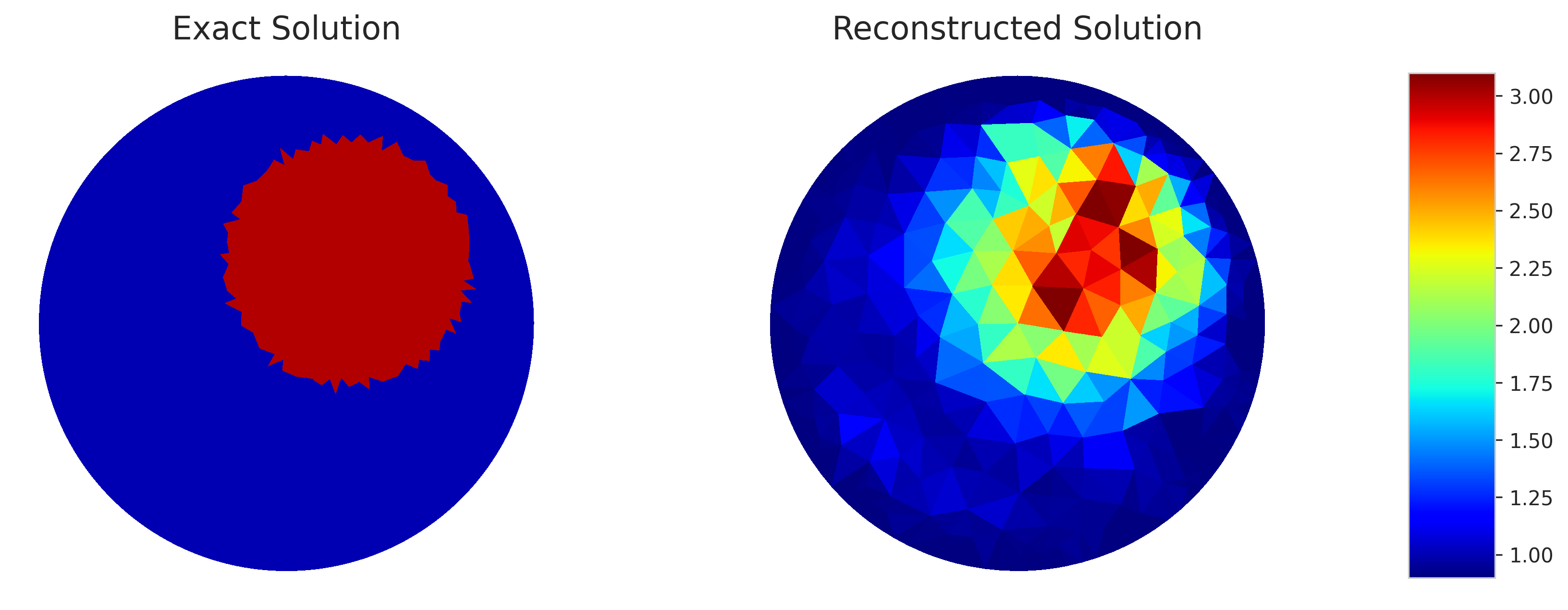
O resultado pode ser extraido utilizando .gamma_k no objeto. A seguir, o plot da solução.:
"Plot result"
gamma_k=InverseObject.gamma_k
V_DG=FiniteElement('DG',mesh_inverse.ufl_cell(),0)
gamma_k=plot_figure(mesh_inverse, V_DG, gamma_k, name=" ");