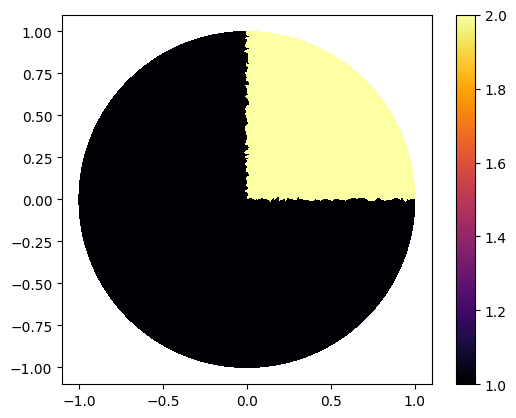Creating Functions

This demo is implemented in a single Python file. tutorial_createfunc.ipynb

This demo illustrates how to:

• How to use GammaCircle().

• Defines its function based on the cells.

• How to use Expression and Conditional Expression.

from module1_mesh import*
from module2_forward import*
from module3_inverse import*
from module4_auxiliar import*
import matplotlib.pyplot as plt
%matplotlib inline

Defining Mesh

"Mesh"
ele_pos=electrodes_position(L=16, per_cober=0.5, rotate=0)
mesh_inverse=MyMesh(r=1, n=10, n_in=7, n_out=0, electrodes_obj=ele_pos)
mesh_refined=MyMesh(r=1, n=15, n_in=25, n_out=10, electrodes_obj=ele_pos)

"Plot"
plt.figure(figsize=(8, 8))
plt.subplot(1,2,1)
plot(mesh_refined, title="Mesh Refined");
plt.subplot(1,2,2)
plot(mesh_inverse, title="Mesh Inverse");

GammaCircle and plot_figure

ValuesCells0=GammaCircle(mesh_refined,3.0,1.0,0.50, 0.25, 0.25);
Q = FunctionSpace(mesh_refined, "DG", 0) #Define Function space with basis Descontinuous Galerkin
gamma = Function(Q)
gamma.vector()[:]=ValuesCells0


"Plot"
p=plot(gamma, title="")
plot(mesh_refined)
plt.colorbar(p)

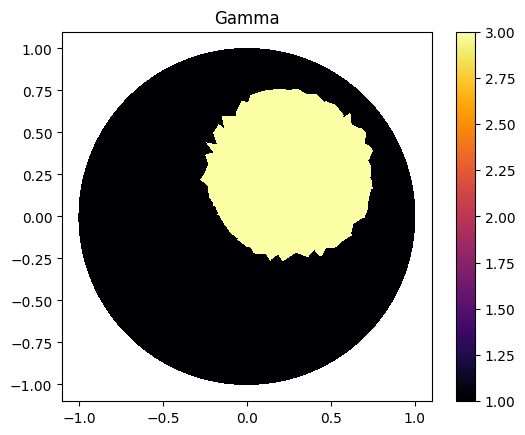
Combining Two Circles

ValuesCells0=GammaCircle(mesh_refined,2.5,0.5,0.30, 0.30, 0.30);
ValuesCells1=GammaCircle(mesh_refined,0.0,0.5,0.30, -0.30, -0.30);
gamma.vector()[:]=ValuesCells0+ValuesCells1

plot_figure(gamma, name="", map="inferno");

Refining the Mesh for Best Results

mesh_refined2=MyMesh(r=1, n=50, n_in=25, n_out=10, electrodes_obj=ele_pos)

ValuesCells0=GammaCircle(mesh_refined2,2.5,0.5,0.30, 0.30, 0.30);
ValuesCells1=GammaCircle(mesh_refined2,0.0,0.5,0.30, -0.30, -0.30);
Q2 = FunctionSpace(mesh_refined2, "DG", 0)
gamma2 = Function(Q2)
gamma2.vector()[:]=ValuesCells0+ValuesCells1

plot_figure(gamma2, name="", map="inferno");

GammaRec

def GammaRec(mesh, in_v, out_v, radius,centerx, centery, angle=0, a=1, b=1):
    ValuesGamma=np.zeros(mesh.num_cells())
    centerx_new = centerx*cos(angle)-centery*sin(angle)
    centery_new = centery*cos(angle)+centerx*sin(angle)
    centerx, centery=centerx_new, centery_new

    for i in range(0, mesh.num_cells()):
        cell = Cell(mesh, i)

        vertices=np.array(cell.get_vertex_coordinates())
        x=(vertices[0]+vertices[2]+vertices[4])/3
        y=(vertices[1]+vertices[3]+vertices[5])/3

        "rotation"
        x_new=x*cos(angle)-y*sin(angle)
        y_new=y*cos(angle)+x*sin(angle)
        x,y=x_new,y_new



        if (1/a*abs(x-centerx)>=radius) or 1/b*abs(y-centery)>=radius:
            ValuesGamma[i]=out_v
        else:
            ValuesGamma[i]=in_v

    return ValuesGamma


ValuesCells1=GammaRec(mesh_refined2, 3.0, 1.0, 0.35, 0.3, 0.0, pi/2*0.9, 1.5, 0.5);
ValuesCells2=GammaRec(mesh_refined2,-1.0, 0.0, 0.2, -0.30, -0.30);
ValuesCells3=GammaRec(mesh_refined2,-1.0, 0.0, 0.2, -0.30, 0.30);
gamma2.vector()[:]=ValuesCells1+ValuesCells2+ValuesCells3

plot_figure(gamma2, name="", map="inferno");

Creating Functions Using Expression

def evalinElement(mesh, u, cell_number):
    cell = Cell(mesh, cell_number)
    vertices=np.array(cell.get_vertex_coordinates())
    x=(vertices[0]+vertices[2]+vertices[4])/3
    y=(vertices[1]+vertices[3]+vertices[5])/3

    result=u(x,y)
    return result

func=Expression("pow(x[0],2)-x[1]", degree=2)

mesh=mesh_refined
ValuesCells4=np.zeros(mesh.num_cells())
for cell_index in range(mesh.num_cells()):
    ValuesCells4[cell_index]=evalinElement(mesh, func, cell_index)

gamma.vector()[:]=ValuesCells4

plot_figure(gamma, name="", map="inferno");

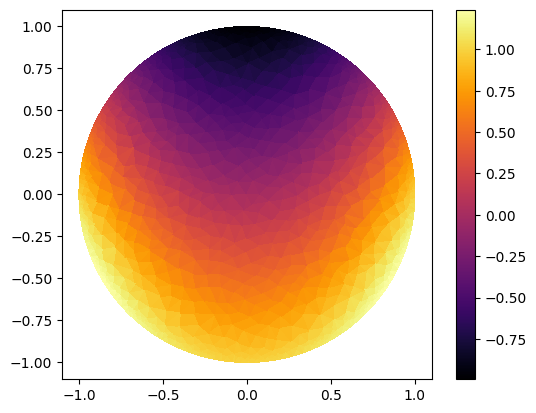
Conditional Expression

func2=Expression("x[1]>= 0 & x[0]>=0 ? 2 : 1 ", degree=2)

mesh=mesh_refined2
ValuesCells5=np.zeros(mesh.num_cells())
for cell_index in range(mesh.num_cells()):
    ValuesCells5[cell_index]=evalinElement(mesh, func2, cell_index)

gamma2.vector()[:]=ValuesCells5
plot_figure(gamma2, name="", map="inferno");