Inverse Problem

This demo is implemented in a single Python file. Download here: tutorial_inverse.ipynb

This demo illustrates how to:

How to use InverseProblem.:

from module1_mesh import*
from module2_forward import*
from module3_inverse import*
from module4_auxiliar import*
import matplotlib.pyplot as plt

Mesh

mesh_inverse, mesh_direct=MyMesh(r=1, n=8, n_vertex=321)
mesh_direct=refine(mesh_direct)

plt.figure(figsize=(8, 8))
plt.subplot(1,2,1)
plot(mesh_direct);
plt.subplot(1,2,2)
plot(mesh_inverse);

Current

"Current"
n_g=6
I_all=current_method(n_g, value=1, method=1)

"Checking hyphotesis"
Verifyg(I_all, mesh_direct)
Verifyg(I_all, mesh_inverse)

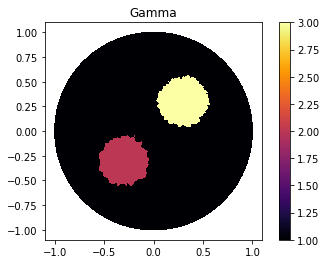
Defining Gamma function

"Defining gamma"
  ValuesCells0=GammaCircle(mesh_direct,3,1,0.35, 0.35, 0.30); #malha, cond_interna, cond_externa, raio.
  gamma0=CellFunction(mesh_direct, values=ValuesCells0);#Pega o vetor e transforma em uma função

  "Plot"
  V_DG=FiniteElement('DG',mesh_inverse.ufl_cell(),0)
  gamma_direct=plot_figure(mesh_direct, V_DG, gamma0, name="Resposta gamma");

Forward Problem

"ForwardProblem"
VD=FiniteElement('CG',mesh_direct.ufl_cell(),1)
ForwardObject=ForwardProblem(mesh_direct)
list_u0=ForwardObject.solve_forward(VD, gamma0, I_all)

u0_boundary=ForwardObject.boundary_array(mesh_inverse) #Boundary data in the mesh_inverse

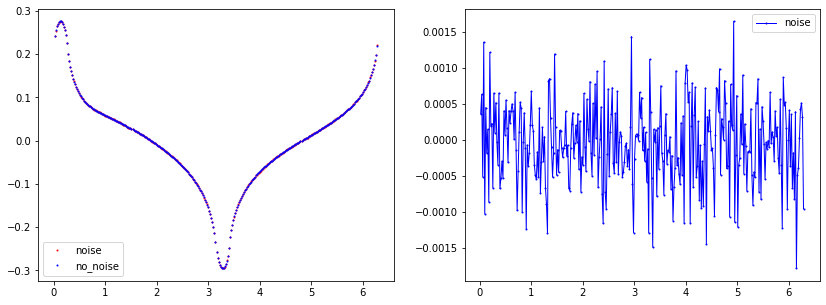
Noise plot

"Noise Parameters"
noise_level=0.005 #0.5%
noise_type='uniform'
seed=1
u0_boundary=ForwardObject.add_noise(noise_level, noise_type, seed, mesh_inverse)

end=len(u0_boundary)
if noise_level>1E-5:
    u0_boundary_c=ForwardObject.boundary_array(mesh_inverse, concatenate=False)
    u_dados_noise=u0_boundary[0:int(end/n_g)]
    data_u0=plot_boundary(mesh_inverse, data=u0_boundary_c[index], name='boundary u0_0', line=0, plot=False)
    data_u0_noise=plot_boundary(mesh_inverse, data=u_dados_noise, name='boundary u0_0', line=0, plot=False)

    plt.figure(figsize=(14, 5))
    plt.subplot(1,2,1)
    plt.plot(data_u0_noise[:,0], data_u0_noise[:,1], linewidth=0,  marker='.', markersize=2, label="noise", color='red');
    plt.plot(data_u0[:,0], data_u0[:,1], linewidth=0,  marker='.', markersize=2, label="no_noise", color="blue");
    plt.legend()

    plt.subplot(1,2,2)
    plt.plot(data_u0[:,0], data_u0[:,1]-data_u0_noise[:,1], linewidth=1,  marker='.', markersize=2, label="noise", color="blue");
    plt.legend()

    plt.show()

Inverse Problem

Inverse Object and Parameters

"Object"
VI=FiniteElement('CG',mesh_inverse.ufl_cell(),1)
InverseObject=InverseProblem(mesh_inverse, VI, u0_boundary, I_all)

"Solver Parameters"
InverseObject.set_solverconfig(step_limit=100)
InverseObject.set_NewtonParameters(mu_i=0.97, mumax=0.999, nu=0.99, R=0.999)
#InverseObject.set_InnerParameters(inner_method='Landweber', land_a=20)
InverseObject.set_InnerParameters(inner_method='ME', ME_reg=5E-3)
#InverseObject.set_InnerParameters(inner_method='CG')
#InverseObject.set_InnerParameters(inner_method='LM', LM_c0=0.95, LM_q=0.05)
#InverseObject.set_InnerParameters(inner_method='Tikhonov', Tik_c0=0.95, Tik_q=0.05)

"Noise Parameters"
tau=1.2
InverseObject.set_NoiseParameters(tau=tau, noise_level=0.005)
print(f"Discrepance stop {tau*noise_level*100}% residue")

"Extra Parameters"
InverseObject.set_answer(gamma0, mesh_direct)
InverseObject.weight_value=False
#MyCellsgamma_k=np.ones(mesh_inverse.num_cells())*2.0
#InverseObject.set_firstguess(MyCellsgamma_k)

Discrepance stop 0.6% residue

#Solver
InverseObject.solve_inverse()

Getting Results

"Getting the result"
gamma_k=InverseObject.gamma_k

"Getting data_summary"
innerstep_vec=InverseObject.innerstep_vec
res_vec=InverseObject.res_vec
mun_vec=InverseObject.mun_vec
error_vec=InverseObject.error_vec

"Plot result"
V_DG=FiniteElement('DG',mesh_inverse.ufl_cell(),0)
gamma_k=plot_figure(mesh_inverse, V_DG, gamma_k, name=" ");

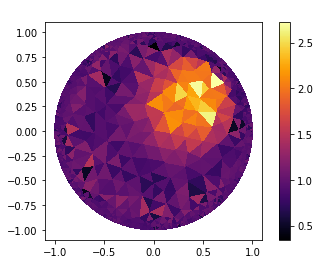
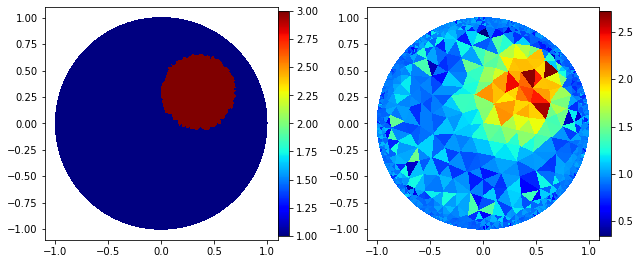
Fancy plot

"Fancy plot"
cmap='jet'
#cmap='inferno'

fig=plt.figure(figsize=(9, 9))
plt.subplot(1,2,1);
p=plot(gamma_direct);
p.set_cmap(cmap)
plt.colorbar(p,fraction=0.046, pad=0.0);

plt.subplot(1,2,2);
p=plot(gamma_k);
p.set_cmap(cmap);
plt.colorbar(p,fraction=0.046, pad=0.0);
fig.tight_layout()

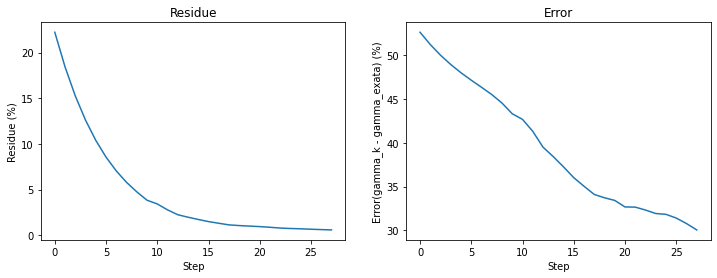
Plot error and residue

plt.figure(figsize=(12, 4));

"Subplot 1"
plt.subplot(1,2,1)
plt.ylabel('Residue (%)');
plt.xlabel('Step');
plt.title('Residue');
plt.plot(range(0,len(res_vec)), res_vec);

"Subplot 2"
plt.subplot(1,2,2)
plt.ylabel('Error(gamma_k - gamma_exata) (%)');
plt.xlabel('Step');
plt.title('Error');
plt.plot(range(0,len(error_vec)), error_vec);

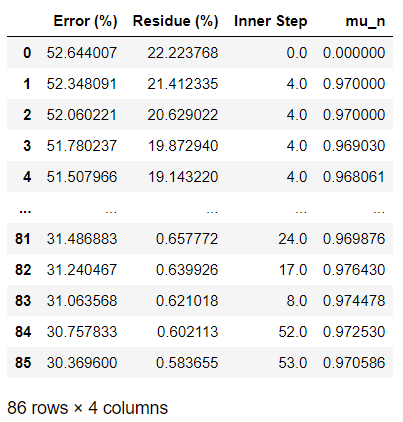
Summary data

summary_data=np.vstack((error_vec, res_vec, innerstep_vec, mun_vec))
data=pd.DataFrame(summary_data.T)
experiments=["Error (%)", "Residue (%) ", "Inner Step", "mu_n"]
data.columns = experiments
data